「資産運用の本質 ファクター投資への体系的アプローチ」を読んでみた
紹介する本
今回は,資産運用の本質 ファクター投資への体系的アプローチ:アンドリュー・アング(著)を紹介したいと思います.
金融に興味を持っている多くの方は資産運用について知りたいという思いがあるかと思います.私の場合,資産運用に興味を持ったことが金融工学を学ぶきっかけでした.そんな折,資産運用の「本質」とまで銘打っているこの本がずっと気になっていました.なかなか高価でしたので購入をためらっていたのですが,今回思い切って買ってみました.800ページを超えているので,まだ途中までしか読んでませんが,現時点での感想を残したいと思います.
本の内容
この本の特徴は,著者が経験した事柄や著者の友人などの経験談から私たちが学ぶべきことは何かを問いかけるように文章が記述されているということです.理論だけを知りたい!という方はこの本の購入はお勧めしません.
前半では,ものすごくざっくりまとめると,「平均・分散ポートフォリオの理論から得ることができる教養は何か」ということに関して実際の出来事を絡めて説明を行なっています.どちらかというと,規範的(理論が正しいと仮定すると,投資家はこのように行動すべき)という立場に立っており,そのようにしなかった企業がどのようになってしまったのか,ということを実例を出して説明する部分が多い気がします.しかし一方で,実際の投資家はこのように行動しているという記述的(データから投資家の行動を逆算し,このように実際は行動している,ということを明らかにする.実証的とも呼ぶ)な立場からの説明もなされており,理論が抱えている仮定について注意すべきである旨も示しており,とてもバランスが良い印象を受けました.
何より,文章がとてもわかりやすく,かつ,面白く描かれていることが素晴らしいと感じました.一章ごとに問題提起から始まり,理論や実例を出して,最後に問題に対する考察がなされています.そして,綺麗に次の章へと移っていき,自分の頭の中に新しい情報が入るが,スッキリ整理されて積み上がっている感覚を受けます.
後半では,本のサブタイトルにもある「ファクター」とは何かについて書かれています.まだ私は後半に突入したばかりなので,うまく感想はかけませんが,前半を見る限り期待できそうです.パラパラめくると,ファーマ・フレンチは当たり前として,他にも様々なファクターについて説明がなされているように見えます.おそらく,ファーマ・フレンチに関しても,私が知らないような情報が多量に説明されているのだと思います.期待しながら読んでいきたいと思います.
最後に
前半しかまだ読んでいませんが,購入する価値があるかという疑問を持っている方がいれば,私個人としては間違いなく買いを勧めます.しかし,途中にも書きましたが,理論のみを追い求める人には向かないとは思います.ただ単純に読み物として面白いです.分厚いですが,ハリーポッターが読めるんだったら,間違いなく読めるでしょう.後半を読み終えたら,また全体の評価・感想について書きたいなぁと思います.
ちなみに
他の本も並行して読んでいるので,そっちの本も紹介していきたいと思います.有名な本からマイナーな本まで手広く紹介できたらいいなぁ.
債券運用と投資戦略
紹介する本
今回紹介するのは,債券運用と投資戦略(第四版):野村證券株式会社 太田智之(監修)です.
株式の運用に関しての理論や実務などを説明している本はとても多いですが,債券の運用について説明している本は比較的少ないのが現状です(特に日本語の本では).その中でも,比較的最近出版されたこの本の帯には「マイナス金利の状況下におけるALMなどのテクニカル面についての進展」のようなとても興味を引く文言が書いてあったので購入してみました.
本の内容
第一章では,日本の債券市場の変遷について説明がなされており,近年の質的・量的金融緩和についても軽くではありますが触れています.どのようにして債券市場が今の形になったのかということに関して知りたいときには,この章を読めばその流れを掴むことはできると思います.
第二章では,債券投資の分析の基礎について書かれています.利回りやデリバティブに関してなど金融工学に少し触れている方なら皆知っているような内容ではありますが,実際のデータを用いたグラフや表などを用いて,理論と現実のギャップはあるか,現実ではこのようになっているなどの実務寄りの視点も入れて文章が書かれているので,付加価値がある章だと感じました.
第三章では,債券ポートフォリオについて説明がされています.マーコヴィッツの平均・分散ポートフォリオなどに触れたことがある方には理論面では退屈な章ではあるかもしれません.しかし,この本は実務の方が書いているという特徴が全面に出ており,所々の文章の中に理論と実務のギャップについて触れているため,一回は読んでみるといいかもしれません(その多くは広く知られている事実ではありますが,その内容の再確認という意味でも有用です).また,負債と資産の両方を見る必要性(ALM)についても触れており,債券をどのように運用するかについても書かれています.例として,基本ではありますが,デュレーションマッチングなどの説明がされています.そして章の最後には,投資先を海外にまで伸ばした債券運用の説明を行なっています.為替の影響はどの程度強いのか,どのようにヘッジすればいいのか,について例を用いて書かれています.
第四章は,実務における言葉の定義や計算の仕方などがまとめられており,実際の現場でどのように計算が行われているのかを軽く知ることができます.実際にはもっと複雑な計算は行なっているとは思いますが,その基礎を学ぶには良い章だと思います.
感想
実務の方が書かれた本だけあって,多くの実例があり,文章の端々に理論とのギャップを感じさせるように書いてあるなぁ,という印象でした.裏では「理論のような綺麗な世界なんて無いんだよ!コンチクショウ!」と思いながら書いたのかなぁと思いながら読んでいました.しかし理論を無視しているわけではなく,うまくバランスをとって使うことが重要である,といったことも主張しているような部分もあり,なかなか上手いなと感じました.この「バランス良く」ということは当たり前のように感じますが,実際の現場で行うとなると,おそらくとてつもなく難しいことなんだろう,と思わせるような本でした.
理論面をもっと知りたいという方が読む本では無いと思いますが,実務ではどのように行なっているのだろうと興味がある方には良いかもしれません.理解とはいかないまでも,感覚を掴むという意味では良い本だと感じました.
一つ残念であったのは,マイナス金利が導入されたことで,実務のリスク管理や債券運用の仕方にどのような問題が生じ,それをどのように解決に導いたのか(または,解決するつもりなのか)についてあまり書かれていなかったことです.私個人としては,その部分が一番興味があった部分だったので少し残念でした.ですが,全体としてはとてもよくまとまっていて,良い本だと感じました.
最後に
私は本を出版するレベルの方に意見するほどのものでは無いです.あくまで感想ですので,そこのところよろしくおねがいします....
OR学会に参加してきた in 沖縄
日記なるものを今までつけたことがない(小学生の頃の夏休みの宿題にも出てなかった気がする)ので,このブログをきっかけに日記をつけてみようと思いますです.
OR学会 in 沖縄
沖縄に遊びに行くためにOR学会へ参加しました!
今の時期だと東京はまだ肌寒い季節ですが,沖縄はちょうど良い気温で快適でした.
自分が研究している分野の大御所が目の前にいる中での発表でしたが,練習通りに発表もできましたし,大御所からも「いい結果だね」と言われたのでめちゃくちゃ嬉しかったです.
沖縄の国際通り
三泊四日の沖縄旅行だったので,国際通りを中心に歩き回ってみました.ぶっちゃけて言うと,お土産屋さんばっかりで,ちんすこうや紅芋タルトばっかり売っていてあまり代わり映えしないなぁ,というような印象でした.もちろん他のお店もたくさんあって,その中でも一番良かったのは「雪花の郷」というかき氷屋さんです.かき氷なんて普段はあまり食べないので味の良し悪しなんてわかるのかなぁ,と思いましたが,間違いなく美味しい!と感じました.
沖縄のいいところ
沖縄っていいなぁ,と思ったのは飯が安いという点です.東京で食べたら1000円余裕で超えるものが700~800円くらいで食べられます.しかも沖縄の方が美味しい(気がする.旅行気分だからかなぁ).後はもちろん気温が穏やかなところと花粉があまり飛んでいないことが素晴らしい.特に後者は私にとってめちゃくちゃ重要です...
最後に
三泊四日と言っても学会に出ている時間もあるので,あまり色々なところを見ることはできなかったけど,それでもいいところだなぁという印象を受けました.国際通りに限ってはもう少しお店のレパートリーが増えたらいいなぁと思います.また,沖縄で学会があったら行きたいですな.
日記ってこんな感じでいいのかわからんけど,とりあえずこれから何かあったら書いていこうと思います.
S&P500と日経225の時系列分析(コピュラ & DCDモデル)
前回 –> コピュラとは(時系列分析・DCDモデルの前準備として) - GRGと金融工学・統計解析
はじめに
前回はコピュラについて簡単に触れましたが,今回はそのコピュラを導入した多変量時系列モデルであるDCDモデルについて見ていきたいと思います.DCDモデルはCopula-Based DCCモデルやCopula GARCHモデルなど様々な呼び方があるそうです.先ずはコピュラを実際のデータに適用して,どのような結果を得ることができるのかについてみていきます.そして,その後にコピュラを組み込んだ多変量の時系列モデルについて説明していきます.
コピュラ
今回は,コピュラの中で基本となる正規コピュラとtコピュラ,そしてアルキメディアンコピュラと呼ばれるクラスに属するクレイトンコピュラ,グンベルコピュラ(ガンベルと呼ぶときもあります)の全部で4つのコピュラを対象にします.前回にも説明をしましたが,自身が持つデータに最適なコピュラを選ぶことはとても難しい問題です.今回は多く用いられている方法の一つであるAICによる比較により,どのコピュラが相応しいかを決定したいと思います.コピュラの推定を行う前に,簡単にそれぞれのコピュラについて簡単な説明をします.
正規コピュラ:相関パラメーター\( \rho \)によって相関を表現します.裾部分の相関についてはあまりうまく表現できません.
tコピュラ:自由度\( \nu \)と相関パラメーター\( \rho \)によって相関を表現します.上側と下側両方の裾部分の相関について表現することができます.しかし,その相関の仕方は上側と下側で同じ強さであることに注意する必要があります.自由度が無限大に近づくことで正規コピュラも表現することができます.
クレイトンコピュラ:下側の裾部分に着目したようなコピュラです.下側の裾部分の相関を捉えることはできますが,上側は捉えることができません.
グンベルコピュラ:上側の裾部分に着目したようなコピュラです.上側の裾部分の相関を捉えることはできますが,下側は捉えることができません.
コピュラのパラメーター推定
RのVineCopulaパッケージを用いて,4つのコピュラのパラメーターの推定と同時にAICの比較を行います.ここで用いるのは最尤推定法ですが,一つ問題があります.それは「それぞれの変数の周辺分布をどのように決めるのか」という問題です.解決の方法としては色々あります.一つがパラメトリックに周辺分布を決定する方法.他には,ノンパラメトリックに周辺分布を推定する方法もあります(間をとったセミパラメトリックな方法というものもあります).立場によって使うべき方法が異なりますが,近年の研究では「コピュラを決めるために自分でコピュラをはじめに選択しているのに(今回の場合,4つのコピュラのこと),周辺分布までパラメトリックに決めてしまってはモデルリスクが高すぎやしないか?」という意見が多いような気がします.そのため,ノンパラメトリックな方法で周辺分布を推定する研究が増えているように感じます.ここでもこの意見に賛成し,ノンパラメトリックな方法で進んで行きましょう.(ちなみに,最尤推定法ではなくケンドールのタウなどを用いてパラメーターを逆算する方法もあります.).周辺分布はRのksパッケージを用いて推定を行います.
d_SP500 <- kcde(Dat[,1]) #S&P500の累積分布関数を推定 d_NIKKEI <- kcde(Dat[,2]) #NIKKEI225の累積分布関数を推定 uni_SP500_data <- predict(d_SP500,x=Dat[,1]) #データを周辺分布を用いて変換する uni_NIKKEI_data <- predict(d_NIKKEI,x=Dat[,2]) #データを周辺分布を用いて変換する copula_select <- BiCopSelect(uni_SP500_data,uni_NIKKEI_data,indeptest = TRUE,familyset = 0:4) #コピュラの推定 summary(copula_select) Family ------ No: 2 Name: t Parameter(s) ------------ par: 0.12 (SE = 0.03) par2: 6.38 (SE = 1.39) Dependence measures ------------------- Kendall's tau: 0.08 (empirical = 0.08, p value < 0.01) Upper TD: 0.05 Lower TD: 0.05 Fit statistics -------------- logLik: 23.9 AIC: -43.8 BIC: -33.64
VineCopulaパッケージのBiCopSelect関数はコピュラのパラメーター推定と,AICによる比較を自動で行ってくれます.その結果より今回選択した4つのコピュラの中で一番AICが低かったコピュラは,tコピュラであることがわかります.パラメータのpar=0.12が相関パラメーターであり,par2=6.38が自由度を表しています.相関パラメーターは正であり,自由度も大きくないことから,S&P500のlog-returnとNIKKEI225のlog-returnは正の関係性があり,片方が大きく変動する時には,もう片方も大きく変動する傾向がある,ということがわかりました.同時に大きく変動する傾向の強さを表しているのが,Upper TDとLower TDです.TDとはTail Dependenceのことで,日本語では裾従属性と呼ばれます.この数値が高いほど,同時に大きく変動する傾向が強いことを意味しています.上述しましたが,今回選ばれたtコピュラは上側と下側の裾の相関の強さは同じとなるコピュラであり,結果からも0.05と同じになっていることが確認できます.
DCDモデル
では次にDCDモデルについてみていきます.DCDモデルはDCCモデルと似ていますが,コピュラを含んでいるので残差項が従う分布が異なります.DCCモデルは相関行列と分散が時間によって変化することで,全体の関係性の時間変化について表現しています.DCDモデルは分散は時間変化しますが,相関自体は変化しません.しかし,その相関の表現の幅をコピュラを用いることでとても広くしていることが特徴です.DCCモデルについては,前の記事を参考にしてください.S&P500と日経225の時系列分析(DCCモデル・多変量GARCH) - GRGと金融工学・統計解析
DCDモデルは次のように表せます.
ここで,\( \epsilon (t) = {\bf D(t)^{-1}u(t)} \)です.では,rmgarchパッケージを用いてパラメーター推定を行なってみましょう.今回は代表として,先ほど選ばれたtコピュラを用いて推定を行なっていきます.
spec_garch = ugarchspec(mean.model = list(armaOrder = c(1,1)), variance.model = list(garchOrder = c(1,1), model = "eGARCH"), distribution.model = "norm") #前回フィットが良かったEGARCHモデルを用いる spec_copula = cgarchspec(uspec = multispec( replicate(2, spec_garch) ), distribution.model = list(copula = "mvt", method = "ML", time.varying = FALSE, transformation = "empirical")) #最尤推定で,時間変化なし,周辺分布はノンパラメトリック(経験分布) fit_dcd_garch = cgarchfit(spec_copula, data = Dat,solver.control=list(trace=1)) #DCDモデルのパラメーター推定 fit_dcd_garch *-------------------------------------------------* * Copula GARCH Fit * *-------------------------------------------------* Distribution : mvt No. of Parameters : 16 [VAR GARCH CC] : [0+14+2] No. of Series : 2 No. of Observations : 1184 Log-Likelihood : 7613.743 Av.Log-Likelihood : 6.431 Optimal Parameters --------------------------------------------------- Estimate Std. Error [SP500_return].mu 0.000436 0.000071 [SP500_return].ar1 0.967133 0.009397 [SP500_return].ma1 -0.989801 0.000019 [SP500_return].omega -1.079997 0.010065 [SP500_return].alpha1 -0.297082 0.021932 [SP500_return].beta1 0.889947 0.000205 [SP500_return].gamma1 0.060124 0.006241 [NIKKEI_return].mu 0.000280 0.000456 [NIKKEI_return].ar1 -0.564162 0.016720 [NIKKEI_return].ma1 0.513227 0.016645 [NIKKEI_return].omega -0.520552 0.192267 [NIKKEI_return].alpha1 -0.100018 0.044924 [NIKKEI_return].beta1 0.938522 0.022040 [NIKKEI_return].gamma1 0.226924 0.039240 [Joint]C1 0.150311 0.029645 [Joint]mshape 21.530978 13.061260 t value Pr(>|t|) [SP500_return].mu 6.1718e+00 0.000000 [SP500_return].ar1 1.0292e+02 0.000000 [SP500_return].ma1 -5.1200e+04 0.000000 [SP500_return].omega -1.0730e+02 0.000000 [SP500_return].alpha1 -1.3546e+01 0.000000 [SP500_return].beta1 4.3407e+03 0.000000 [SP500_return].gamma1 9.6342e+00 0.000000 [NIKKEI_return].mu 6.1457e-01 0.538840 [NIKKEI_return].ar1 -3.3741e+01 0.000000 [NIKKEI_return].ma1 3.0834e+01 0.000000 [NIKKEI_return].omega -2.7074e+00 0.006780 [NIKKEI_return].alpha1 -2.2264e+00 0.025989 [NIKKEI_return].beta1 4.2583e+01 0.000000 [NIKKEI_return].gamma1 5.7830e+00 0.000000 [Joint]C1 5.0703e+00 0.000000 [Joint]mshape 1.6485e+00 0.099258 Information Criteria --------------------- Akaike -12.834 Bayes -12.765 Shibata -12.834 Hannan-Quinn -12.808 Elapsed time : 4.794555
ここでは,[Joint]と書いてある部分に着目してみます.C1が相関パラメーター,mshapeが自由度を表しています.相関パラメーターは先ほどの結果と同じような大きさですが,自由度は大きくなっていることがわかります.先ほどは個々の分散について時間変化を考えていなかったため,同時に大きく動く可能性について自由度を小さくすることで調整していたと考えられます(自由度を小さくすると,裾部分の相関が増えるため).しかし分散が時間変化することを許すことで,同時に大きく動く可能性を分散によって表現することができるようになり,自由度が大きくなったと考えられます.
Dynamic DCD モデル
DCDモデルだけでもとても柔軟な表現をすることができますが,やはり相関がどのように時間変化するか,といったことを調べることは重要です.DCDモデルのコピュラのパラメーターを変化させることで相関の動きを表すことができたら,DCCモデルよりも広い範囲の相関を見ることができます.先ほどのRのコードを見た時にお気づきかもしれませんが,rmgarchパッケージはその時間変化を考慮したDynamic DCDモデルの推定も行うことができます.先ほどのコードのtime.varying=FALSEの部分をTRUEにするだけで,実際に分析を行うことができます.用意したデータを用いて推定した結果は次のようになりました.
*-------------------------------------------------* * Copula GARCH Fit * *-------------------------------------------------* Distribution : mvt DCC Order : 1 1 Asymmetric : FALSE No. of Parameters : 18 [VAR GARCH DCC UncQ]: [0+14+3+1] No. of Series : 2 No. of Observations : 1184 Log-Likelihood : 7613.966 Av.Log-Likelihood : 6.431 Optimal Parameters --------------------------------------------------- Estimate Std. Error [SP500_return].mu 0.000436 0.000072 [SP500_return].ar1 0.967133 0.009710 [SP500_return].ma1 -0.989801 0.000020 [SP500_return].omega -1.079997 0.009890 [SP500_return].alpha1 -0.297082 0.022440 [SP500_return].beta1 0.889947 0.000213 [SP500_return].gamma1 0.060124 0.006279 [NIKKEI_return].mu 0.000280 0.000452 [NIKKEI_return].ar1 -0.564162 0.016562 [NIKKEI_return].ma1 0.513227 0.016645 [NIKKEI_return].omega -0.520552 0.188960 [NIKKEI_return].alpha1 -0.100018 0.045090 [NIKKEI_return].beta1 0.938522 0.021669 [NIKKEI_return].gamma1 0.226924 0.039257 [Joint]dcca1 0.013889 0.027853 [Joint]dccb1 0.679697 0.813742 [Joint]mshape 22.527427 31.755845 t value Pr(>|t|) [SP500_return].mu 6.0610e+00 0.000000 [SP500_return].ar1 9.9599e+01 0.000000 [SP500_return].ma1 -5.0386e+04 0.000000 [SP500_return].omega -1.0920e+02 0.000000 [SP500_return].alpha1 -1.3239e+01 0.000000 [SP500_return].beta1 4.1755e+03 0.000000 [SP500_return].gamma1 9.5759e+00 0.000000 [NIKKEI_return].mu 6.1906e-01 0.535879 [NIKKEI_return].ar1 -3.4064e+01 0.000000 [NIKKEI_return].ma1 3.0833e+01 0.000000 [NIKKEI_return].omega -2.7548e+00 0.005872 [NIKKEI_return].alpha1 -2.2182e+00 0.026543 [NIKKEI_return].beta1 4.3311e+01 0.000000 [NIKKEI_return].gamma1 5.7805e+00 0.000000 [Joint]dcca1 4.9865e-01 0.618026 [Joint]dccb1 8.3527e-01 0.403564 [Joint]mshape 7.0939e-01 0.478080 Information Criteria --------------------- Akaike -12.833 Bayes -12.760 Shibata -12.833 Hannan-Quinn -12.805 Elapsed time : 5.495759
AICを見ると,ほんの少しではありますが,時間変化なしのDCDモデルの方が低いという結果になりました.このことから,時間変化を考慮することは大きく精度が向上するわけではないことがわかりました(今回のデータセットの場合は,ということに注意).しかし,Dynamicにすることで相関の時間変化について図示することができるようになります.その結果が次のグラフです.DCCモデルと比較するために下図に,前回の結果を載せてみました(上図のグラフは相関パラメーターのものなので実際にはDCCモデルと直接比較することは避けた方がいいかもしれません.).


tコピュラの相関パラメーターの変動がDCCモデルの結果と同じように大きいということは,変数同士が同時に大きく変動する傾向も大きく動いていることも意味しています.なぜなら,先ほど説明したTail Dependenceは相関パラメーターと大きな関係があるからです.tコピュラの場合,相関パラメーターが高くなるとTDも高くなります.
Dynamic DCDモデルはとても柔軟なモデルであり,これ以上追加したら複雑なモデルになりすぎてしまいます(できないことはないが,パラメーターの推定精度が心配).では,Dynamic DCDモデルは利点だらけのモデルなのかというと,やはりそうではありません.はじめに挙げられる欠点としては,DCDモデルはコピュラの欠点を引き継いでいるという点です.そして,変数が増えるとパラメータ数が急激に増えるので,パラメーター推定に時間がかかったり,推定の精度が悪くなりがちです.このような欠点を加味すると,CCCモデルやDCCモデルの方を用いる方がいい時もありますので注意が必要です.
まとめ
今回ははじめに前回触れたコピュラを実際のデータに当てはめて結果を確認しました.その結果tコピュラが選択した4つのコピュラの中で最適であることがわかりました.その後,DCDモデルやDynamic DCDモデルのパラメーター推定を行い,時間変化を考慮しても今回はAICは大きく向上しなかったことや,DCCモデルの結果と同様に相関が時間によって大きく変化していることが明らかとなりました.DCDモデルは利点も多いですが,欠点も少なからずあるので,注意して使用していきましょう.
次回の予定は考えていませんが,興味があるものがたくさんあるので,それらの紹介をしていけたらなぁと思います.
コピュラとは(時系列分析・DCDモデルの前準備として)
前回 –> S&P500と日経225の時系列分析(DCCモデル・多変量GARCH) - GRGと金融工学・統計解析
はじめに
前回はDCCモデルを用いて,S&P500のlog-returnと日経225のlog-returnの相関関係について調べてみました.今回は,DCDモデル(Dynamic Conditional Dependence Model)に必要となってくるコピュラについて説明していきたいと思います.コピュラ自体がとても奥が深くて面白い分野ですので,今後もコピュラに対する,またはコピュラを利用した様々な研究が出てくると思います.ここでは,そのほんの表面部分について見ていきたいと思います.
コピュラとは
コピュラは周辺分布を接合することで新たな多変量分布を作り出すための道具であるため,接合関数とも呼ばれています.例えば,基本的に私たちは多変量正規分布を使ってシミュレーションなど行っています(俺はt分布やskewed-t分布を使っているぜ,NIGも使うぞという方もいるかもしれませんが,例ですので...).しかし,その多変量正規分布はどのように作られているのでしょうか?その答えをくれるのが,スクラーの定理です.
ここで\( F \)は\( F_1 ,F_2 , \dots , F_d \)を周辺分布とする同時分布関数です.周辺分布が連続であるならば,コピュラ\( C \)は一意的に求まることが知られています.では,(1)式は何を意味しているのでしょうか?それは,同時分布\( F \)(例だと,多変量正規分布)は,コピュラ\( C \)と周辺分布\( F_1 ,F_2 , \dots , F_d \)で構成されているということです.逆に言うと,周辺分布とコピュラさえわかってしまえば同時分布を算出することができるということです.例の場合,周辺分布を正規分布,コピュラを正規コピュラと呼ばれるコピュラを選択することで多変量正規分布を構築することができます.
例では多変量正規分布を用いて説明しましたが,多変量t分布でも同じことが言えます.周辺分布をt分布,コピュラをtコピュラと呼ばれるものを選択すると,多変量t分布を構築することができます.つまり,コピュラとは周辺分布を同時分布にまとめ上げるための「繋ぎ」の役割をしていると考えることができます.面白いことに,コピュラによってその繋ぎ方の特徴が異なっていることがわかっています.例えば,正規コピュラよりもtコピュラの方が,周辺分布の裾の部分を繋ぐ力が強いことが知られています.つまり,片方の変数が大きい値をとるときに,もう片方の変数も大きい値をとるようにtコピュラは変数同士を結びつけます.そのことを見るためにRのVineCopulaパッケージを用いて図を用意しました.(このパッケージは研究でも使ったので,親しみがありますなぁ...)
#コピュラの描写 norm_copula <- BiCop(1,par = 0.8) #正規コピュラの設定 t_copula <- BiCop(2,par = 0.8,par2 = 3) #tコピュラの設定 plot(norm_copula,type="contour") plot(t_copula,type="contour")


この二つの図は,周辺分布を標準正規分布として正規コピュラとtコピュラで結びつけたものです(上図:正規コピュラ,下図:tコピュラ).図を見ると,tコピュラの方が先っぽが尖っていることがわかると思います.これはその分だけ裾の関係性が強いということを意味しています.
コピュラが強力な道具である理由として,データにフィットする同時分布を一度に考えるのではなく,周辺分布は周辺分布,コピュラはコピュラでそれぞれ最適なものを選ぶことで,とても幅広い同時分布を扱うことができるという点があります(先ほども同じようなことを記述しましたが,重要なことなのでもう一度).例として,周辺分布は正規分布が最適であり,コピュラはtコピュラが最適であるような場合には,同時分布は多変量正規分布でも多変量t分布でもない複雑なものになります.コピュラを用いることで,同時分布をボトムアップのような形で記述できることは色々な面で役に立ちます.
依存関係(Dependence)と相関関係(Correlation)
コピュラは変数同士の繋ぎの役割をしているということはイメージが持てたと思います.ということは,コピュラは相関関係を考えているのでしょうか.実は,コピュラは相関関係というよりは.依存関係を表していると考えるべきものなのです.では,その相関関係と依存関係は何が違うのかということに関して見ていきます.ここで言及しておきますが,多くの人と話した経験上,各々が持っている相関関係や依存関係の定義が異なることがあります.今回説明するのは,あくまで私個人の考えであるということだけ注意していただきたいと思います.おそらくこの相関関係と依存関係の違いがイメージができたらコピュラの理解の助けになるのではないかと思います.
私の中では,相関関係は周辺分布に関して考慮せずに変数間の関係を見たもの,というイメージを持っています.一方,依存関係は周辺分布を考慮した変数間の関係を見たもの,というイメージです.例を用意したので,それを用いてもう少し細かく説明します.
#シミュレーションによる周辺分布が相関に与える影響 ## 相関関係について norm_dist_1 <- rnorm(100) #標準正規分布から100個サンプリング norm_dist_2 <- rnorm(100) #標準正規分布から100個サンプリング norm_dist_1 <- c(norm_dist_1,8) #恣意的ではあるが,一点だけサンプルを与える norm_dist_2 <- c(norm_dist_2,8) #恣意的ではあるが,一点だけサンプルを与える plot(norm_dist_1,norm_dist_2) lm_sim <- lm(norm_dist_2~norm_dist_1) summary(lm_sim) ## 依存関係について d_norm_1 <- kcde(norm_dist_1) #周辺分布をカーネル密度関数を用いて推定 d_norm_2 <- kcde(norm_dist_2) #周辺分布をカーネル密度関数を用いて推定 uni_norm_1 <- predict(d_norm_1,x=norm_dist_1) # F(x_1)を算出 uni_norm_2 <- predict(d_norm_2,x=norm_dist_2) #F(x_2)を算出 plot(uni_norm_1,uni_norm_2) uni_lm_sim <- lm(uni_norm_2~uni_norm_1) summary(uni_lm_sim)
このシミュレーションは,独立である2つの標準正規分布から100個サンプリングしたものに,一つだけ大きな点を加えたときにどのように関係性を評価してしまうのかを調べることを目的としています.途中でサンプルに(8,8)という点を加えていますが,リーマンショックのようなショックがただ一回だけ起きたと考えてみてください.普段は全く関係性がないもの同士だが,一回だけ揃って大きくなることがあっただけで相関関係がある!と言っていいのでしょうか?(個人的にはそうではないと考えます)
線形回帰を用いて二つの変数の関係を見てみると,次のようになります.(相関係数と回帰係数は似ていますが、異なるものです. 本来なら相関係数を見るべきかもしれませんが、ここでは簡単で直感的な回帰係数を見る事にします)
summary(lm_sim) #結果のサマリー Call: lm(formula = norm_dist_2 ~ norm_dist_1) Residuals: Min 1Q Median 3Q Max -3.2957 -0.7255 -0.1697 0.7369 4.8082 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.23692 0.12144 1.951 0.053901 . norm_dist_1 0.36936 0.09979 3.701 0.000353 *** <-- 有意になっている!! --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.21 on 99 degrees of freedom Multiple R-squared: 0.1216, Adjusted R-squared: 0.1127 F-statistic: 13.7 on 1 and 99 DF, p-value: 0.0003528
点が一つ増えただけですが,強い正の関係性があるというような結果になっていることがわかります.ですが,個人的にはなんか釈然としません.(私だけでしょうか...?)では,依存関係ではどうでしょうか.依存関係を見るときには,周辺分布を推定し,それぞれの変数を\( F_1 (x_1) , F_2 (x_2) \)へと変換したものの関係性を調べる必要があります.今回は,周辺分布をRのksパッケージを用いて推定し,関係性については相関関係と比較するために線形回帰を使ってみます.
summary(uni_lm_sim) #結果のサマリー Call: lm(formula = uni_norm_2 ~ uni_norm_1) Residuals: Min 1Q Median 3Q Max -0.49935 -0.21031 0.00756 0.25115 0.48098 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.49138 0.05793 8.482 2.2e-13 *** uni_norm_1 0.02515 0.10048 0.250 0.803 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.2813 on 99 degrees of freedom Multiple R-squared: 0.0006325, Adjusted R-squared: -0.009462 F-statistic: 0.06266 on 1 and 99 DF, p-value: 0.8029
結果から,二つの変数には関係性がない(有意ではない)ことがわかります.なぜ,このような結果となったのでしょうか?それはもちろん周辺分布を考慮したからです.散布図を見てみるとよりわかりやすいと思います.
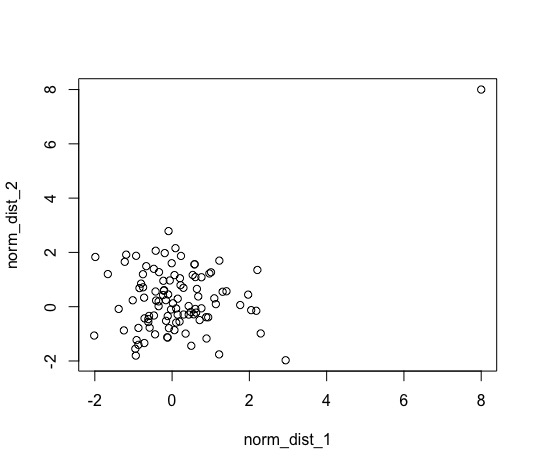
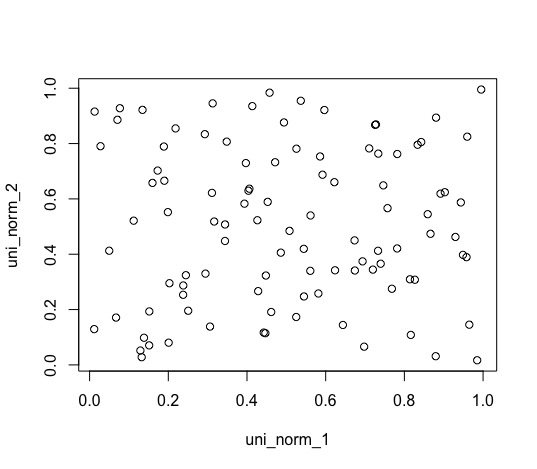
上図が周辺分布を考慮していない生データの散布図であり,下図が周辺分布をかませた散布図となっています.この例は少し大げさではありますが,実際に起きてしまう可能性もあることは認識する必要があります.周辺分布の裾が長ければ,その分この例のようなことが起こりえます.そのため,周辺分布をかませて裾の影響を無くした変数同士の関係性を見ることで,より深くその関係性を見ることができます.普通は周辺分布をかましてから線形回帰を行うことは少ないと思いますが(もし行うとしたら,分位点回帰であるべき),直感的な理解には役立ちます.本来なら,周辺分布をかませたデータを用いてコピュラのパラメータを推定する流れとなります.
長くなりましたが結果から,周辺分布を考慮して関係性を見ることで変数間の関係性をより深く見ることができそうです.そして,その関係性のことを従属関係と呼びます(私は呼んでいます,といったほうがいいかもしれません).この従属関係を得てから,周辺分布の影響をそれぞれの変数に戻すことで,相関関係をみることもできます.もし,そのような手順を踏んだ場合,単純な線形相関関係ではなく,非線形な相関関係を見ていたことに気付くと思います(このような手順を踏んで相関関係を見る手法をコピュラ回帰と呼びます.ある条件を満たしていたら,非線形ではなく線形のままの関係性を見ることもできます).
従属関係と相関関係はとても似ているため混在してしまうかもしれません.しかし,ここでは紹介していない従属関係ならではの指標(裾従属性など)もあるため,従属関係は相関関係よりもっと広い範囲を意味していることは言及しておきます.
コピュラの欠点
今まではコピュラの良いところしか述べていませんでしたが,もちろん欠点もあります.それは,コピュラにはとても多くの種類があり,それぞれ異なった特徴を持っていますが,自分が持っているデータだけ見てもどのコピュラが最適なのかがわからない,という点です.通常は最大尤度やAICなどの指標を使って判断します.
最後に
今回は,コピュラについて触れてみました.例などは2変量しか使っていませんでしたが,もっと多変量になるケースが多いとおもいます.その際には,Vine Copula(ヴァイン・コピュラ)などの柔軟性がものすごく高いコピュラ(の組み立て方)を用いることができます.次回は,DCDモデルについて見ていきたいと思います.
S&P500と日経225の時系列分析(DCCモデル・多変量GARCH)
前回 –> S&P500と日経225の時系列分析(単変量GARCH) - GRGと金融工学・統計解析
はじめに
前回は単変量のGARCHモデルについて触れました.今回は,多変量に拡張したGARCHモデルについて触れていきます.多変量になったとしても,単変量の時とほとんど同じような議論をすることができます.しかし,多変量になることで相関関係を考える必要が出てくるので,そのモデリングの仕方が重要となってきます.そこで今回は,Dynamic Conditional Correlation Model(DCCモデル)を用いて相関関係を見ていきます.
DCCモデル
まずは,DCCモデルについて見てみましょう.多変量の時系列モデルは一般的に次のように書けます.
DCCモデルは(1)式の\( H(t) \)のモデリングを行います.\( H(t) \)の対角成分は各変数の分散となるので,前回紹介したGARCHモデルやEGARCHモデルなどを用いて表現することができます.問題なのは,対角成分以外の成分(共分散)をどのように表現するかです.DCCモデルでは次のように表現しています.
ここで\( \epsilon (t-1) = {\bf D(t)^{-1}u(t)} \)であり,\( \bar{Q} \)は\( \epsilon (t) \)の条件なし相関行列を意味しています.いきなり数式が色々出てきましたが,一つずつ見ていきましょう.(2)式は\( D(t), R(t) \)の組み合わせですが,(3)式にあるように\( D(t) \)は各変数の標準偏差を対角成分に持つ行列で,\( R(t) \)は相関行列を意味しています.そのため,(2)式のように掛け合わされると,分散共分散行列\( H(t) \)が出てくるという関係となっています.相関行列\( R(t) \)は行列Qで特徴付けられていて,Qが変化することでRが変化するような構造になっています.そして,そのQの動きを表したのが(5)式という形です.\( R(t) \)が相関行列になるためには,(5)式のパラメータが,\(0 \leq a, 0 \leq b, a+ b < 1 \)となる必要があります.
初見だと,なかなかに複雑なモデルだと感じるかもしれません.もし扱うことが難しそうだと感じるならば,DCCモデルではなく,CCCモデルで慣れてから使うといいかもしれません.CCCモデルは,Constant Conditional Correlation Modelの略称で,相関行列が時間に依存せずに一定である,というような仮定を置いたモデルとなっています.つまり,
という形となっています.\( D(t) \)が変化することにより,間接的に共分散が動くようなモデルとなっています.とても単純で,使いやすいという理由から広く利用されているモデルです.
DCCモデルのパラメータ推定
では,2012-03-07から2017-03-07のS&P500のlog-returnと日経225のlog-returnの関係をDCCモデルを用いて分析してみます.使うパッケージはRのrmgarchパッケージです.
#DCCモデル spec_garch = ugarchspec(mean.model = list(armaOrder = c(1, 1),include.mean=TRUE), variance.model = list(garchOrder = c(1,1), model = 'eGARCH'), distribution.model = 'norm') spec_multi = multispec(replicate(2, spec_garch)) spec_dcc = dccspec(uspec = spec_multi, dccOrder = c(1, 1), distribution = "mvnorm",model = "DCC") fit_dcc_garch = dccfit(spec_dcc, data = Dat, fit.control = list(eval.se = TRUE)) SP500_NIKKEI_cor <- as.vector(rcor(fit_dcc_garch)[1,2,]) SP500_vola <- as.vector(sigma(fit_dcc_garch)[,1]) NIKKEI_vola <- as.vector(sigma(fit_dcc_garch)[,2])
各変数のボラティリティはEGARCHモデルで記述しています.これは,前回EGARCHモデルが一番AICが低かったことからそのようにしています.(ちなみに,EGARCHモデルはGARCHモデルを特別な場合として含んでいないため,AICで比較することが正しいとは言えないかもしれません.もっと多角的な評価が本当は必要です.)ここでは,基本的なモデルとして全ての分布が正規分布であるとおいています.
まず,相関係数はどのような変動をしているのかを見てみます.

時間によって大きく変化していることがわかります.また,ほぼ全ての期間で相関係数が正であることも見て取れます.次に,それぞれのボラティリティも見てみます.


ボラティリティも大きく変動していることがわかります.以上の結果から,やはりボラティリティや相関係数が一定という仮定を置いて,ポートフォリオを組むことはあまりいいことではないことがわかります.(しかし,ポートフォリオ問題を複雑にし過ぎるのもよくはない.そこが難しいところですよねぇ...)
最後に
次回は,Dynamic Conditional Dependence Model(DCDモデル)について触れていきたいと思います.もしかしたら,コピュラの説明が長くなってしまい,コピュラの回になってしまうかもしれませんが...もっとわかりやすく人に伝えられる文章を書けるように頑張ります!
参考文献
沖本竜義:経済・ファイナンスデータの計量時系列分析
S&P500と日経225の時系列分析(単変量GARCH)
今回は,GARCH周りについて触れていきます.データは,S&P500と日経225の2012-03-07から2017-03-07の期間のlog-returnを用いて最近の挙動について調べていきます.
GARCHモデルはボラティリティに着目したモデルです.前回まではVARモデルを用いて平均について着目していましたが,今回はボラティリティに着目する点に注意しましょう.では,なぜボラティリティに着目する必要があるのでしょうか.その答えの一つとして,株価の変動は一時期において大きく変動する傾向が続くことが知られているからということが挙げられます.このことをボラティリティクラスタリングと呼びます.実際のデータから実証的に得られたこのstylized factを表現するためにボラティリティに着目する必要性があるのです.または,前回説明したエントロピーに関する情報量についてより深く知るため,と考えても良いかもしれません.単変量のGARCH(1,1)モデルは以下のように表せる.
GARCH(1,1)の(1,1)とは,(2)式のボラティリティ項hとホワイトノイズ項uを一時点前のものを一つずつ用いることを意味しています.このように,ボラティリティ項がARモデルのようになっているものをGARCH(1,1)モデルと呼びます.(1)式の\( \mu (t) \)をARモデルやARMAモデルなどに設定したものを,AR-GARCHモデルやARMA-GARCHモデルと呼んだりします.今までの流れとして,GARCHモデルを用いる際には天下り的にGARCH(1,1)モデルが使われることが多いです.GARCH(1,1)モデルでも柔軟な表現がすることができることからきているのだと思われます.
GARCHモデルはとても柔軟性があり,広く使われていますが,それでもまだ表現できていないstylized factがあります.それは,ボラティリティの撹乱項\( u(t-1) \)がボラティリティに与える影響は正の時より負の時の方が大きいという点です.このことをレバレッジ効果と呼びます.この性質を表すために,GJRモデルと呼ばれるGARCHモデルを拡張したモデルが提案されています.GJRモデルでは,以下のようにボラティリティが変動します.
ここで,\( I(t-1) \)は\( u(t-1) \)が負の時に1となり,それ以外の時には0になる指示関数です.(3)式のように指示関数をおくことで,\( u(t-1) \)が負の時にだけ,係数が\( \alpha + \gamma \)となり\( \gamma \)が正であれば先ほどのstylized factが説明できるだろうというようなモデルとなります.他にも,ボラティリティのモデルの中ではExponential GARCHモデル(EGARCHモデル)がよく使われています.
(4)式がEGARCHモデルと呼ばれるものです.今までとは異なり,(1)式の\( \nu (t-1) \)がボラティリティ項に含まれています.\( \gamma \nu (t-1) \)は,\( \gamma \)が負であれば,株価が減少するとボラティリティが上昇するということを表しています.\( \delta ( |\nu (t-1)| - E(|\nu (t-1)|)) \)は,\( \nu (t-1) \)に対する期待される値からの実現値のズレがボラティリティに与える影響を表しています.\( \delta \)が正であれば,ズレが大きくなるとボラティリティが大きくなるという直感的に正しいモデルとなります.
では,Rを使ってそれぞれのモデルのパラメータを推定してみましょう.Rのrugarchパッケージを使って推定を行っていきます.まずは,S&P500のlog-returnのデータを用いて推定してみます.
spec_garch <- ugarchspec( #GARCHモデルについての情報を入力 variance.model = list(model = "sGARCH", garchOrder=c(1,1)), mean.model = list(armaOrder = c(1,1), arfima = F), distribution.model = "norm") spec_gjr <- ugarchspec( #GJRモデルについての情報を入力 variance.model = list(model = "fGARCH", garchOrder=c(1,1),submodel="GJRGARCH"), mean.model = list(armaOrder = c(1,1), arfima = F), distribution.model = "norm") spec_egarch <- ugarchspec( #EGARCHモデルについての情報を入力 variance.model = list(model = "eGARCH", garchOrder=c(1,1)), mean.model = list(armaOrder = c(1,1), arfima = F), distribution.model = "norm") #パラメータ推定 (Dat[,1]の中にS&P500のlog-returnのデータが入っている) fit_garch <- ugarchfit(spec_garch, Dat[,1]) fit_gjr <- ugarchfit(spec_gjr, Dat[,1]) fit_egarch <- ugarchfit(spec_egarch, Dat[,1]) #AICの表示 infocriteria(fit_garch)[1] [1] -6.940626 #GARCHモデルのAIC infocriteria(fit_gjr)[1] [1] -6.979851 #GJRモデルのAIC infocriteria(fit_egarch)[1] [1] -7.012425 #EGARCHモデルのAIC
AICを見る限り,EGARCHモデルが三つのモデルの中で一番良いモデルというような結果であることがわかります.では,パラメータは上述のような関係になっているのでしょうか.GJRモデルと,EGARCHモデルのパラメータ推定の結果を見てみましょう.
#GJRモデルのパラメーター Optimal Parameters ------------------------------------ Estimate Std. Error t value Pr(>|t|) mu 0.000527 0.000053 9.8679e+00 0 ar1 0.951819 0.006746 1.4110e+02 0 ma1 -0.986672 0.000002 -6.0180e+05 0 omega 0.000007 0.000000 9.2706e+01 0 alpha1 0.071451 0.010597 6.7424e+00 0 beta1 0.744011 0.016680 4.4604e+01 0 eta11 0.998444 0.004455 2.2412e+02 0 Robust Standard Errors: Estimate Std. Error t value Pr(>|t|) mu 0.000527 0.000056 9.4219e+00 0e+00 ar1 0.951819 0.005809 1.6385e+02 0e+00 ma1 -0.986672 0.000000 -9.8033e+06 0e+00 omega 0.000007 0.000000 1.1079e+02 0e+00 alpha1 0.071451 0.015291 4.6728e+00 3e-06 beta1 0.744011 0.031136 2.3896e+01 0e+00 eta11 0.998444 0.002659 3.7556e+02 0e+00 LogLikelihood : 4139.072 #EGARCHモデルのパラメーター Optimal Parameters ------------------------------------ Estimate Std. Error t value Pr(>|t|) mu 0.000436 0.000006 72.345 0 ar1 0.967133 0.006571 147.181 0 ma1 -0.989801 0.000015 -65586.909 0 omega -1.079997 0.006710 -160.955 0 alpha1 -0.297082 0.015141 -19.620 0 beta1 0.889947 0.000140 6344.786 0 gamma1 0.060124 0.004725 12.724 0 Robust Standard Errors: Estimate Std. Error t value Pr(>|t|) mu 0.000436 0.000074 5.8744 0 ar1 0.967133 0.008901 108.6502 0 ma1 -0.989801 0.000018 -54909.0351 0 omega -1.079997 0.010441 -103.4423 0 alpha1 -0.297082 0.022451 -13.2323 0 beta1 0.889947 0.000197 4511.0978 0 gamma1 0.060124 0.006936 8.6680 0 LogLikelihood : 4158.356
GJRモデルの場合,eta11というパラメータが(3)式の\( \gamma \)を意味しており,期待通り正となっていることがわかります.EGARCHモデルの場合,(4)式の\( \gamma \)が結果の\( \alpha 1 \)となり,\( \delta \)が\( \gamma 1 \)に対応しています.結果から,EGARCHモデルについても期待通りの符号であったということが言えそうです.この結果はS&P500の結果ですが,日経225の結果も同じように期待通りにパラメータの符号となり,EGARCHモデルが一番AICが小さかったことがわかりました.(結果は長くなってしまうので省略します.)
次は,多変量のGARCHモデル関係について触れていきます.例えば,DCC-GARCHやコピュラを含んだ柔軟性がとても高い多変量のモデルの紹介をしていきます.