コピュラとは（時系列分析・DCDモデルの前準備として）

前回 –> S&P500と日経225の時系列分析（DCCモデル・多変量GARCH） - GRGと金融工学・統計解析

はじめに

前回はDCCモデルを用いて，S&P500のlog-returnと日経225のlog-returnの相関関係について調べてみました．今回は，DCDモデル（Dynamic Conditional Dependence Model）に必要となってくるコピュラについて説明していきたいと思います．コピュラ自体がとても奥が深くて面白い分野ですので，今後もコピュラに対する，またはコピュラを利用した様々な研究が出てくると思います．ここでは，そのほんの表面部分について見ていきたいと思います．

コピュラとは

コピュラは周辺分布を接合することで新たな多変量分布を作り出すための道具であるため，接合関数とも呼ばれています．例えば，基本的に私たちは多変量正規分布を使ってシミュレーションなど行っています（俺はt分布やskewed-t分布を使っているぜ，NIGも使うぞという方もいるかもしれませんが，例ですので．．．）．しかし，その多変量正規分布はどのように作られているのでしょうか？その答えをくれるのが，スクラーの定理です．

ここで\( F \)は\( F_1 ,F_2 , \dots , F_d \)を周辺分布とする同時分布関数です．周辺分布が連続であるならば，コピュラ\( C \)は一意的に求まることが知られています．では，(1)式は何を意味しているのでしょうか？それは，同時分布\( F \)（例だと，多変量正規分布）は，コピュラ\( C \)と周辺分布\( F_1 ,F_2 , \dots , F_d \)で構成されているということです．逆に言うと，周辺分布とコピュラさえわかってしまえば同時分布を算出することができるということです．例の場合，周辺分布を正規分布，コピュラを正規コピュラと呼ばれるコピュラを選択することで多変量正規分布を構築することができます．

例では多変量正規分布を用いて説明しましたが，多変量t分布でも同じことが言えます．周辺分布をt分布，コピュラをtコピュラと呼ばれるものを選択すると，多変量t分布を構築することができます．つまり，コピュラとは周辺分布を同時分布にまとめ上げるための「繋ぎ」の役割をしていると考えることができます．面白いことに，コピュラによってその繋ぎ方の特徴が異なっていることがわかっています．例えば，正規コピュラよりもtコピュラの方が，周辺分布の裾の部分を繋ぐ力が強いことが知られています．つまり，片方の変数が大きい値をとるときに，もう片方の変数も大きい値をとるようにtコピュラは変数同士を結びつけます．そのことを見るためにRのVineCopulaパッケージを用いて図を用意しました．（このパッケージは研究でも使ったので，親しみがありますなぁ．．．）

#コピュラの描写

norm_copula <- BiCop(1,par = 0.8) #正規コピュラの設定
t_copula <- BiCop(2,par = 0.8,par2 = 3) #tコピュラの設定
plot(norm_copula,type="contour")
plot(t_copula,type="contour")

この二つの図は，周辺分布を標準正規分布として正規コピュラとtコピュラで結びつけたものです（上図：正規コピュラ，下図：tコピュラ）．図を見ると，tコピュラの方が先っぽが尖っていることがわかると思います．これはその分だけ裾の関係性が強いということを意味しています．

コピュラが強力な道具である理由として，データにフィットする同時分布を一度に考えるのではなく，周辺分布は周辺分布，コピュラはコピュラでそれぞれ最適なものを選ぶことで，とても幅広い同時分布を扱うことができるという点があります（先ほども同じようなことを記述しましたが，重要なことなのでもう一度）．例として，周辺分布は正規分布が最適であり，コピュラはtコピュラが最適であるような場合には，同時分布は多変量正規分布でも多変量t分布でもない複雑なものになります．コピュラを用いることで，同時分布をボトムアップのような形で記述できることは色々な面で役に立ちます．

依存関係（Dependence）と相関関係（Correlation）

コピュラは変数同士の繋ぎの役割をしているということはイメージが持てたと思います．ということは，コピュラは相関関係を考えているのでしょうか．実は，コピュラは相関関係というよりは．依存関係を表していると考えるべきものなのです．では，その相関関係と依存関係は何が違うのかということに関して見ていきます．ここで言及しておきますが，多くの人と話した経験上，各々が持っている相関関係や依存関係の定義が異なることがあります．今回説明するのは，あくまで私個人の考えであるということだけ注意していただきたいと思います．おそらくこの相関関係と依存関係の違いがイメージができたらコピュラの理解の助けになるのではないかと思います．

私の中では，相関関係は周辺分布に関して考慮せずに変数間の関係を見たもの，というイメージを持っています．一方，依存関係は周辺分布を考慮した変数間の関係を見たもの，というイメージです．例を用意したので，それを用いてもう少し細かく説明します．

#シミュレーションによる周辺分布が相関に与える影響

## 相関関係について

norm_dist_1 <- rnorm(100) #標準正規分布から100個サンプリング
norm_dist_2 <- rnorm(100) #標準正規分布から100個サンプリング
norm_dist_1 <- c(norm_dist_1,8) #恣意的ではあるが，一点だけサンプルを与える
norm_dist_2 <- c(norm_dist_2,8) #恣意的ではあるが，一点だけサンプルを与える

plot(norm_dist_1,norm_dist_2)
lm_sim <- lm(norm_dist_2~norm_dist_1)
summary(lm_sim)

## 依存関係について

d_norm_1 <- kcde(norm_dist_1) #周辺分布をカーネル密度関数を用いて推定
d_norm_2 <- kcde(norm_dist_2) #周辺分布をカーネル密度関数を用いて推定
uni_norm_1 <- predict(d_norm_1,x=norm_dist_1) # F(x_1)を算出
uni_norm_2 <- predict(d_norm_2,x=norm_dist_2) #F(x_2)を算出

plot(uni_norm_1,uni_norm_2)
uni_lm_sim <- lm(uni_norm_2~uni_norm_1)
summary(uni_lm_sim)

このシミュレーションは，独立である2つの標準正規分布から100個サンプリングしたものに，一つだけ大きな点を加えたときにどのように関係性を評価してしまうのかを調べることを目的としています．途中でサンプルに(8,8)という点を加えていますが，リーマンショックのようなショックがただ一回だけ起きたと考えてみてください．普段は全く関係性がないもの同士だが，一回だけ揃って大きくなることがあっただけで相関関係がある！と言っていいのでしょうか？（個人的にはそうではないと考えます）

線形回帰を用いて二つの変数の関係を見てみると，次のようになります．(相関係数と回帰係数は似ていますが、異なるものです. 本来なら相関係数を見るべきかもしれませんが、ここでは簡単で直感的な回帰係数を見る事にします)

summary(lm_sim) #結果のサマリー

Call:
lm(formula = norm_dist_2 ~ norm_dist_1)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.2957 -0.7255 -0.1697  0.7369  4.8082 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.23692    0.12144   1.951 0.053901 .  
norm_dist_1  0.36936    0.09979   3.701 0.000353 ***   <-- 有意になっている！！
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.21 on 99 degrees of freedom
Multiple R-squared:  0.1216, Adjusted R-squared:  0.1127 
F-statistic:  13.7 on 1 and 99 DF,  p-value: 0.0003528

点が一つ増えただけですが，強い正の関係性があるというような結果になっていることがわかります．ですが，個人的にはなんか釈然としません．（私だけでしょうか．．．？）では，依存関係ではどうでしょうか．依存関係を見るときには，周辺分布を推定し，それぞれの変数を\( F_1 (x_1) , F_2 (x_2) \)へと変換したものの関係性を調べる必要があります．今回は，周辺分布をRのksパッケージを用いて推定し，関係性については相関関係と比較するために線形回帰を使ってみます．

summary(uni_lm_sim) #結果のサマリー

Call:
lm(formula = uni_norm_2 ~ uni_norm_1)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.49935 -0.21031  0.00756  0.25115  0.48098 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.49138    0.05793   8.482  2.2e-13 ***
uni_norm_1   0.02515    0.10048   0.250    0.803    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2813 on 99 degrees of freedom
Multiple R-squared:  0.0006325,  Adjusted R-squared:  -0.009462 
F-statistic: 0.06266 on 1 and 99 DF,  p-value: 0.8029

結果から，二つの変数には関係性がない（有意ではない）ことがわかります．なぜ，このような結果となったのでしょうか？それはもちろん周辺分布を考慮したからです．散布図を見てみるとよりわかりやすいと思います．

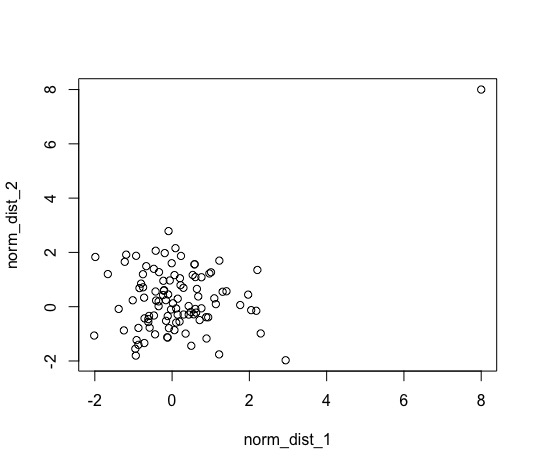
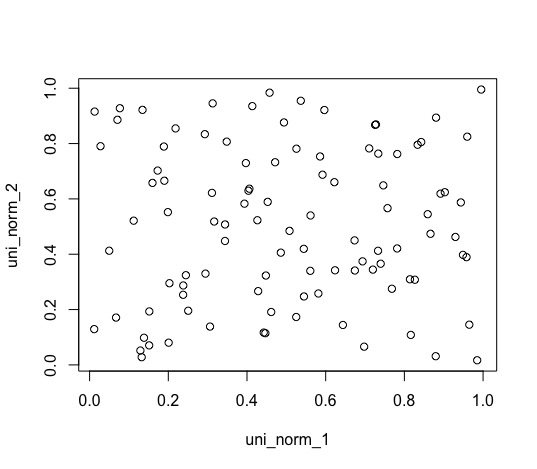
上図が周辺分布を考慮していない生データの散布図であり，下図が周辺分布をかませた散布図となっています．この例は少し大げさではありますが，実際に起きてしまう可能性もあることは認識する必要があります．周辺分布の裾が長ければ，その分この例のようなことが起こりえます．そのため，周辺分布をかませて裾の影響を無くした変数同士の関係性を見ることで，より深くその関係性を見ることができます．普通は周辺分布をかましてから線形回帰を行うことは少ないと思いますが（もし行うとしたら，分位点回帰であるべき），直感的な理解には役立ちます．本来なら，周辺分布をかませたデータを用いてコピュラのパラメータを推定する流れとなります．

長くなりましたが結果から，周辺分布を考慮して関係性を見ることで変数間の関係性をより深く見ることができそうです．そして，その関係性のことを従属関係と呼びます（私は呼んでいます，といったほうがいいかもしれません）．この従属関係を得てから，周辺分布の影響をそれぞれの変数に戻すことで，相関関係をみることもできます．もし，そのような手順を踏んだ場合，単純な線形相関関係ではなく，非線形な相関関係を見ていたことに気付くと思います（このような手順を踏んで相関関係を見る手法をコピュラ回帰と呼びます．ある条件を満たしていたら，非線形ではなく線形のままの関係性を見ることもできます）．

従属関係と相関関係はとても似ているため混在してしまうかもしれません．しかし，ここでは紹介していない従属関係ならではの指標（裾従属性など）もあるため，従属関係は相関関係よりもっと広い範囲を意味していることは言及しておきます．

コピュラの欠点

今まではコピュラの良いところしか述べていませんでしたが，もちろん欠点もあります．それは，コピュラにはとても多くの種類があり，それぞれ異なった特徴を持っていますが，自分が持っているデータだけ見てもどのコピュラが最適なのかがわからない，という点です．通常は最大尤度やAICなどの指標を使って判断します．

最後に

今回は，コピュラについて触れてみました．例などは2変量しか使っていませんでしたが，もっと多変量になるケースが多いとおもいます．その際には，Vine Copula（ヴァイン・コピュラ）などの柔軟性がものすごく高いコピュラ（の組み立て方）を用いることができます．次回は，DCDモデルについて見ていきたいと思います．